Sorting Algorithms: HeapSort

tags : algorithms,sorting,divide-and-conquer, level: ha, medium

From the array create a max heap (largest element at the top). Then do an in place sortdown of the heap.

Heap

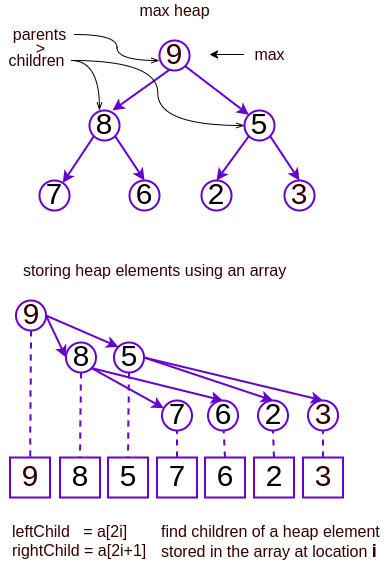
max-heap: A binary tree with a property that
every parent is > both children.

The largest element is at the top of the heap.

Heapsort is named such because it uses heap datastructure.

create a max-heap from the array
In Place SortDown, iteratively delete the max from the heap and place it or at end of the unsorted array
at the start of the sorted array

// Pseudo code

Create-Max-Heap(A)
// In-Place Sortdown
for (i=A.length; i>=2; i--) {
    swap (A[1], A[i])
    A.heapSize--
    max-heapify(A,1)
}

heap

Heapsort Implementation

  
  
heapSort(a) {
  // Create a max-heap
  heapSize = a.length;
  for(i=heapSize/2, i>=1, i--) {
      maxHeapify(a,i)
  }
  // one at a time
  // delete max element from heap
  int maxHeapElement = 1;
  for(i=a.length; i>=0; i--){
    swap(a[maxHeapElement], a[i])
    maxHeapify(a,n, heapsize--)
  }
}

private void maxHeapify(a[],int i, int heapSize)
{
    while (2*i <= heapSize) {

     int left = 2*i;
     int right = left+1;
     int largest = left; // assume left is largest
     
     // which child is grater left or right ?
     if (left < heapSize && a[left] < a[right])
         largest = right; 

     // a[i] is at correct position, exit
     if (a[i] > largest)) break;

     swap (a[i], a[largest]);
     i = largest;
    }
}

Heapsort Visualization

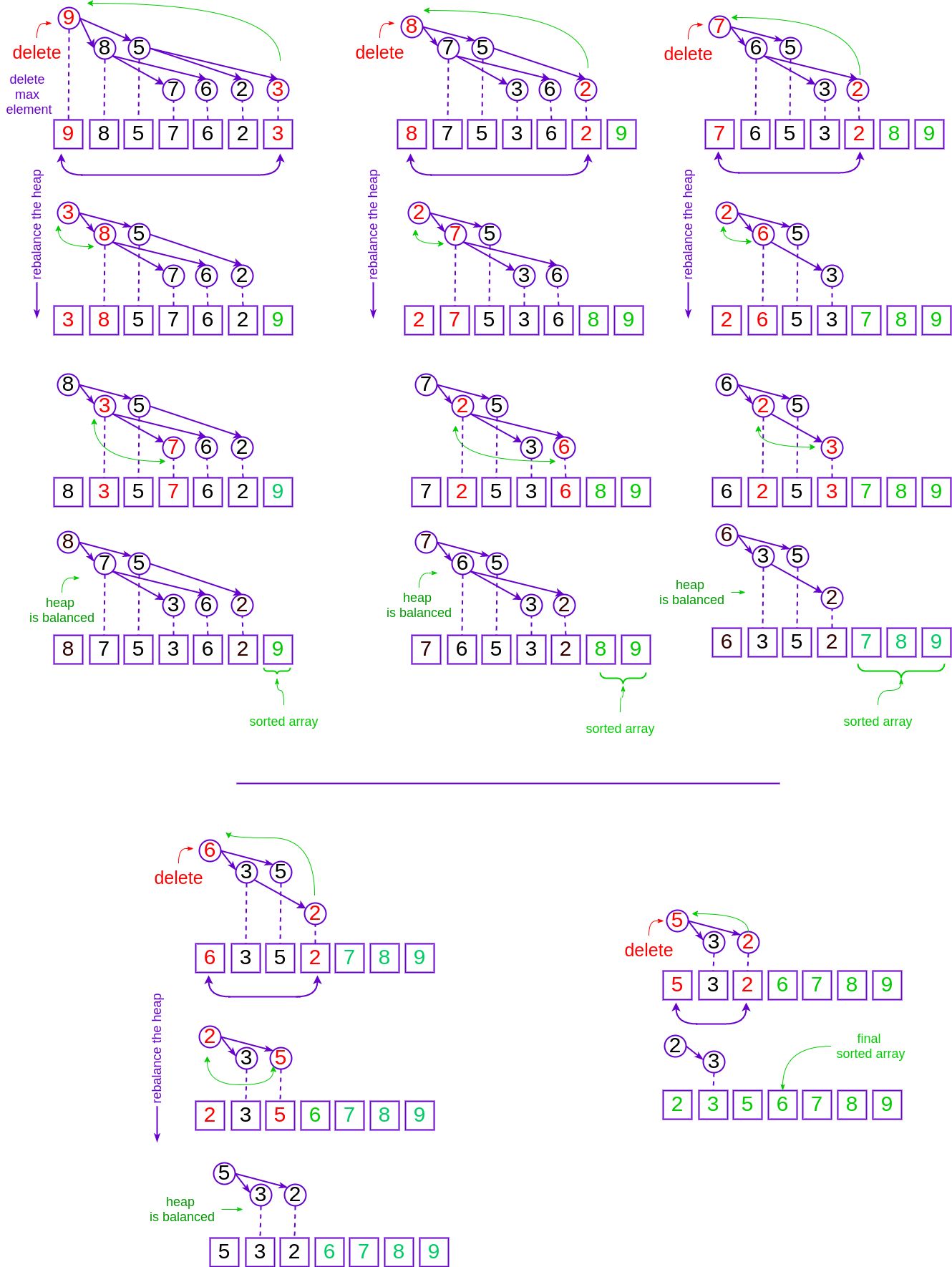
heapsort

Running time

Best case

$O(nlog(n))$

Worst case

$O(nlog(n))$

Space complexity

$O(1)$

Sorter coder