Merge sort is a divide and conquer algorithm which divides the array into 2 arrays, sort those 2 arrays recursively using merge sort and merge the results.
The core algorithm in merge sort is "how to merge two already sorted arrays into a new sorted array".
Merging two pre sorted arrays
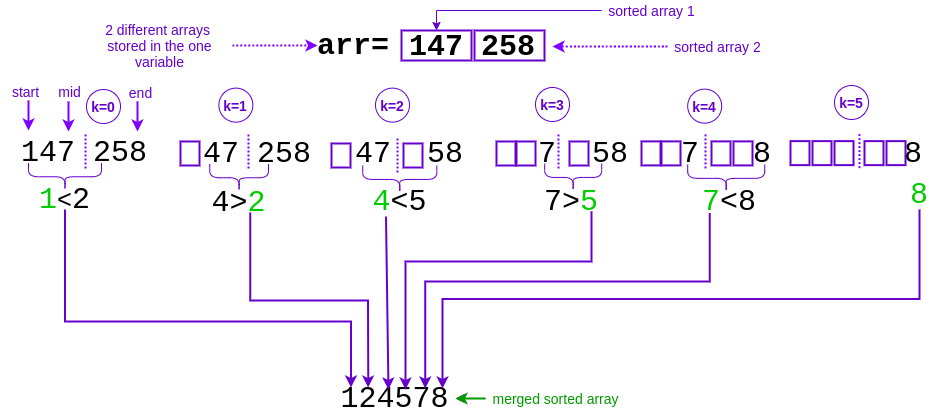
// array 1 - array[start-mid]
// array 2 - array[start-end]
merge(array[], start, mid ,end) {
int[] tmp = Arrays.copyOf(array)
int i=start; int j=mid+1;
for(int k=start; k<end; k++) { // merging
if (i>mid) array[k] = tmp[j++]
else if (j>end) array[k] = tmp[i++]
else if (a[j]<a[i]) array[k] = tmp[j++]
else array[k] = tmp[i++]
}
}Algorithm to merge 2 already sorted arrays
In each iteration {
- get smaller element of the 2 arrays
-
if one of the arrays becomes empty {
then there is no decision to make
simply copy element from remaining array
}
}
Top down merge sort
mergeSort(array[], start, end) {
if (start < end) {
mid = (start + end)/2;
mergeSort(array, start, mid - 1);
mergeSort(array, mid + 1, end);
merge(array, start , mid, end);
} else { // recursion reaches an end
return;
}
}
// array 1 - array[start-mid]
// array 2 - array[start-end]
merge(array[], start, mid ,end) {
int[] tmp = Arrays.copyOf(array)
int i=start; int j=mid+1;
for(int k=start; k<end; k++) { // merging
if (i>mid) array[k] = tmp[j++]
else if (j>end) array[k] = tmp[i++]
else if (a[j]<a[i]) array[k] = tmp[j++]
else array[k] = tmp[i++]
}
}
Bottom up merge sort
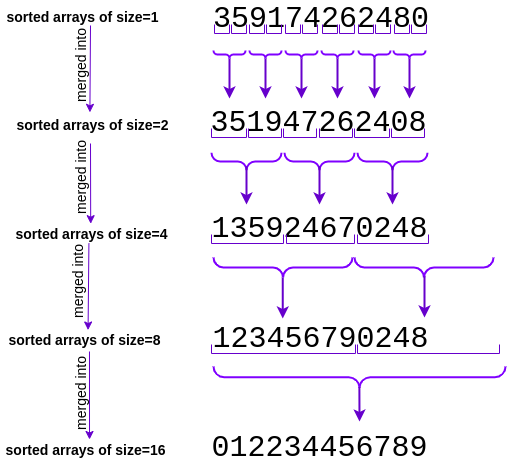
mergeSort(int[] array) {
int length = array.length;
for (int step=1; step<length; step=2*step) {
for (int i=0; i<length; i+=2*step) {
merge(array,
i, // start
i+step-1, // mid
min(i+2*step, N-1) ) // end of sub-array
}
}
}
// array 1 - array[start-mid]
// array 2 - array[start-end]
merge(array[], start, mid ,end) {
int[] tmp = Arrays.copyOf(array)
int i=start; int j=mid+1;
for(int k=start; k<end; k++) { // merging
if (i>mid) array[k] = tmp[j++]
else if (j>end) array[k] = tmp[i++]
else if (a[j]<a[i]) array[k] = tmp[j++]
else array[k] = tmp[i++]
}
}
Running time
Best case
In any divide and conquer algorithm the best case is when the each subproblem is size n/2.
Worst case
References
Berkley Merge Sort
Khan Academy Quicksort Analysis
Khan Academy Quicksort Overview
Duke university lecture notes